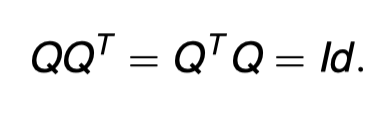Slides 15
vector space
矢量空间的线性表示
A vector space is a mathematical structure formed by two types of objects: a collection of elements called vectors, and two operations on pairs of vectors: addition and scalar multiplication. As such two vectors may be added together, and any vector can be multiplied by numbers, called scalars. Thus, for a vector space X, for any two of its elements x, y ∈ X, and any numbers α, β ∈ F (a field of numbers), we can form the linear combinations as new elements of X:
矢量空间是由两类对象形成的数学结构:称为矢量的元素集合,以及对矢量对的两种操作:加法和标量乘法。因此,两个向量可以相加,任何向量都可以与数字相乘,称为标量。因此,对于一个矢量空间X,对于它的任何两个元素x,y∈X,以及任何数字α,β∈F(一个数域),我们可以形成线性组合作为X的新元素。
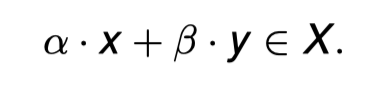
矢量空间的公理
The operations of addition and scalar multiplication in a vector space must satisfy a number of conditions called axioms:
Associativity of addition
Commutativity of addition
Identity element of addition
Inverse elements of addition
Compatibility of scalar multiplication with field multiplication Identity element of scalar multiplication
Distributivity of scalar multiplication with respect to vector addition Distributivity of scalar multiplication with respect to field addition
矢量空间中的加法和标量乘法运算必须满足一些条件,称为公理。
加法的关联性
加法的共轭性
加法的同一元素
加法的逆向元素
标量乘法与字段乘法的相容性
标量乘法的身份元素
标量乘法对于矢量加法的分布性
标量乘法对于场加法的分布性
A basis is a set of linearly independent vectors which can represent every vector in a given vector space through their linear combinations.
An orthogonal basis for a vector space with an inner product, is a basis with vectors which are mutually orthogonal (perpendicular). If the vectors of an orthogonal basis are or length (norm) 1, the resulting basis is an orthonormal basis (ONB).
An ONB may cease to be an ONB after even a small perturbation, or when any of its elements is removed. We seek thus representation systems with more stability.
Frames were introduced by Dunford and Schaeffer in 1952.
基是一组线性独立的向量,它可以通过它们的线性组合代表给定向量空间中的每个向量。
一个具有内积的向量空间的正交基,是一个具有相互正交(垂直)的向量的基。如果一个正交基的向量都是长度(规范)为1的,那么得到的基就是一个正交基(ONB)。
一个ONB甚至在一个小的扰动之后,或者当它的任何元素被移除之后,都可能不再是一个ONB。因此,我们寻求具有更多稳定性的表示系统。
框架是由邓福德和谢弗在1952年提出的。
The role of a basis is to allow us to represent elements of the vector space in terms of sequences of scalars (numbers), which are called vector coordinates. This is an important step, because thanks to this representation, abstract or complicated objects obtain a uniform mathematical format. The reason for this may not necessarily be clear when we think of the most typical example of a vector space: d-dimensional Euclidean vector space. This is because the Euclidean space is not just a good example of a vector space, it is also a prototypical example, and last but not least - a finite dimensional vector space.
Infinite dimensional vector spaces provide us with more intriguing examples of objects, and the role of a basis which allows us to replace these complicated objects by sequences of numbers becomes much more clear.
Vector spaces of polynomials;
Function spaces (Lipschitz, integrable, finite energy functions, etc.)
基的作用是允许我们用标量(数字)的序列来表示矢量空间的元素,这些标量被称为矢量坐标。这是重要的一步,因为有了这种表示方法,抽象或复杂的对象就获得了统一的数学格式。当我们想到矢量空间最典型的例子时,可能不一定清楚其中的原因:D维欧几里得矢量空间。这是因为欧几里得空间不仅是矢量空间的一个很好的例子,它也是一个典型的例子,最后但并非最不重要的是–一个一维矢量空间。
几何维向量空间为我们提供了更多有趣的对象例子,而基础的作用使我们能够用数字序列来取代这些复杂的对象,这一点变得更加清晰。
多项式的矢量空间。
函数空间(Lipschitz、可整定、限定能量的函数等)
A norm in a vector space X is a non-negative real-valued function x ↦ → ∥ x ∥ , which satisfies the axioms of sublinearlity (also known as Minkowski inequality or triangle inequality), and non-degeneracy.
A normed vector space is a pair ( X, ∥ · ∥) where X is a vector space and ∥ · ∥ a norm on X.
Every finite (N) dimensional vector space X can be equipped with a norm. Indeed, let { b 1 , . . . , b N } be a basis for X. Then, for any x ∈ X, we can write uniquely:
矢量空间X中的规范是一个非负实值函数x ↦ → ∥ x ∥ ,它满足次线性公理(也称为明斯基不等式或三角不等式)和非退化性公理。
规范化向量空间是一对( X, ∥ - ∥),其中X是一个向量空间,∥ - ∥是X上的规范。
每个有限的(N)维向量空间X都可以配备一个规范。事实上,让{b 1 , … … 然后,对于任何x∈X,我们可以写出唯一的。
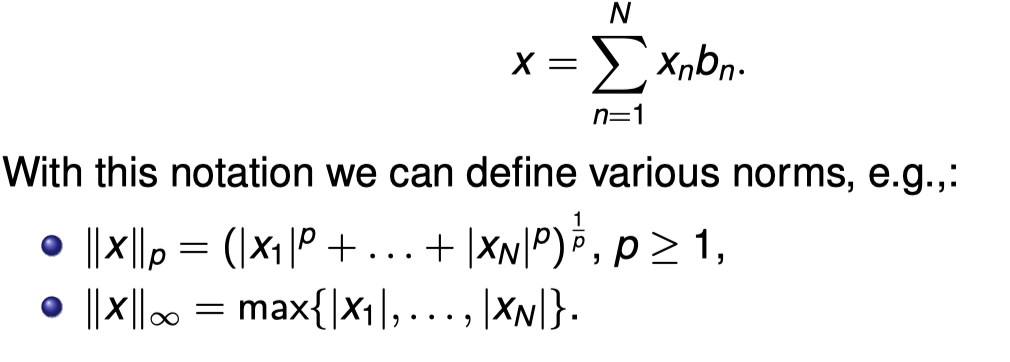
Example: Fourier Basis for RN
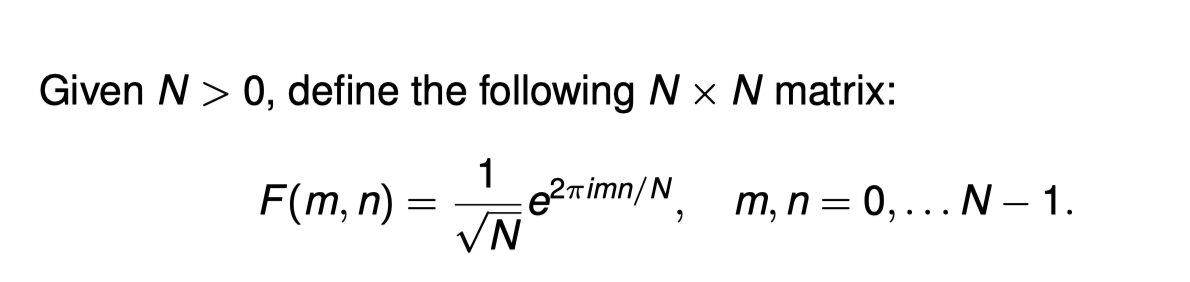
The columns (or rows) of this matrix form an orthonormal basis for the space of N-dimensional complex vectors R N . This basis is called the Fourier basis. And the matrix F is known as the Discrete Fourier Transform. Clearly F is a unitary matrix, and as such it is, in particular, invertible.
这个矩阵的列(或行)构成了N维复数向量空间R N的正态基。这个基被称为傅里叶基。而矩阵F被称为离散傅里叶变换。显然,F是一个单元矩阵,因此,它尤其是可反转的。
The dimension theorem for vector spaces states that all bases of a vector space have equally many elements.
This unique number of elements for a given vector space may be finite or infinite.
We define the dimension of the vector space to be the number of elements of any its basis.
It is sometimes called the Hamel dimension.
We are interested in finite dimensional vector spaces.
A Euclidean vector space is a finite-dimensional inner product space over the real numbers.
A typical case of Euclidean vector space is R n . Every Euclidean space is isomorphic to this example.
维度向量空间的维度定理指出,向量空间的所有基数都有同样多的元素。
对于一个给定的向量空间来说,这个唯一的元素数可能是无限的,也可能是不确定的。
我们将矢量空间的维数定义为其任何基的元素数。
它有时被称为Hamel维度。
我们感兴趣的是finite维度的向量空间。
欧几里得向量空间是实数上的一个五维内积空间。
欧氏矢量空间的一个典型案例是R n。每个欧几里得空间都与这个例子同构。
Eigenvalues and Eigenvectors
特征值和特征向量
If A is a linear transformation from a vector space R n into itself and v = 0 is a nonzero vector in V, then v is an eigenvector of T if T ( v ) ̸ is a scalar multiple of v, for some λ ∈ R,
In this case we say that λ is the eigenvalue (characteristic value) of A associated with v.
There is a direct correspondence between n × n matrices and linear transformations from R n into itself, given any basis of the vector space. Hence, in a finite-dimensional vector space, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices, or the language of linear transformations.
如果A是一个从矢量空间R n到自身的线性变换,并且v = 0是V中的一个非零矢量,那么如果T ( v ) ̸是v的标量倍数,对于某些λ∈R,v是T的一个特征向量。
在这种情况下,我们说λ是与v相关的A的特征值(特性值)。
在给定矢量空间的任何基础的情况下,n×n矩阵与从R n到自身的线性变换之间存在着直接的对应关系。因此,在finite-dimensional矢量空间中,使用矩阵语言或线性变换语言来定义特征值和特征向量是等价的。
EVD
归一化
The eigendecomposition (EVD) (spectral decomposition) of a matrix is the factorization of this matrix into a canonical form, where the matrix is represented in terms of its eigenvalues and eigenvectors.
If A is a linear transformation from a vector space R n into itself, represented by an n × n matrix, which has n linearly independent eigenvectors e i , i = 1, . . . , n, then A can be written as
矩阵的eigendecomposition(EVD)(谱系分解)是将该矩阵分解为一个典型的形式,其中矩阵以其特征值和特征向量表示。
如果A是一个从矢量空间R n到自身的线性变换,由一个n×n矩阵表示,它有n个线性独立的特征向量e i,i = 1, . . , n,那么A可以被写成
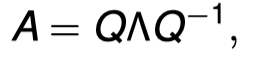
Q is the n × n matrix whose ith column is the eigenvector e i of A;
Λ is the diagonal matrix whose diagonal elements are the corresponding eigenvalues λ i .
Q是n×n矩阵,其第i列是A的特征向量e i;
Λ是对角矩阵,其对角线元素是相应的特征值λ i。
Using EVDs
Suppose we are given data set in the form of an n × m matrix X, where the data points are considered to be the consecutive columns of the matrix X. This means we have m vectors x i in R n (or n observed variables with m independent observations). Next, suppose we use one of the above methods, e.g., PCA, to compute a new ONB for our space R n . Further, assume that these eigenvectors are stored as columns of some matrix V.
假设我们得到了n×m矩阵X形式的数据集,其中数据点被认为是矩阵X的连续列。这意味着我们在R n中有m个向量x i(或n个观察变量有m个独立的观察值)。接下来,假设我们使用上述方法之一,例如PCA,为我们的空间R n计算一个新的ONB。此外,假设这些特征向量被存储为某个矩阵V的列。
We can use the new basis to represent the original data in these new coordinates, i.e., to compute the expansions of the data vectors in terms of the new ONB. To do this we compute:
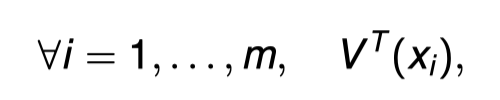
that is we are computing projections of x i onto the basis { v j , j = 1, . . . , n } . In matrix notation V T X is an n × m matrix consisting of column vectors which are the new coefficients of x i ’s in the basis { v j } . This is the desired new representation of our data.
我们可以使用新的基础来表示这些新坐标中的原始数据,即计算数据向量在新的ONB方面的扩展。要做到这一点,我们要计算。
也就是说,我们要计算x i在基{v j , j = 1, . . , n } . 在矩阵符号中,V T X是一个n×m的矩阵,由列向量组成,是x i在基{v j }上的新系数。. 这就是我们所期望的数据的新表示。
特征向量的正态基
Given any eigenvalue λ, we can define its eigenspace to be the collection of vectors for which this is an eigenvalue.
The example with scalar multiplication implies that any multiple of an eigenvector of λ is an eigenvector of λ. Similarly with vector addition. As such an eigenspace is a linear subspace of R n .
If a matrix A satisfies the condition A T A = AA T , then such a matrix has an eigenbasis consisting of mutually orthogonal eigenvectors. This means that eigenspaces are pairwise orthogonal.
This implies that for such an A the matrix Q in EVD is an orthogonal matrix, i.e., such that
给定任何一个特征值λ,我们可以把它的特征空间定义为这是一个特征值的向量的集合。
标量乘法的例子意味着λ的特征向量的任何倍数都是λ的特征向量,与之类似的是向量加法。因此,一个特征空间是R n的一个线性子空间。
如果一个矩阵A满足条件A T A = AA T,那么这样的矩阵就有一个由相互正交的特征向量组成的特征基。这意味着,特征空间是成对正交的。
这意味着对于这样一个A,EVD中的矩阵Q是一个正交矩阵,即,这样的矩阵